Список задач-игр, в которых доказательство выигрыша одной из сторон не использует существование явной стратегии.

Задача 1. Дана шоколадка m на n (m,n > 1). Двое по очереди выбирают точку на пересечении вертикальной и горизонтальной борозд и отламывают левую нижнюю часть шоколадки. Каждым ходом должно быть отломано ненулевое число долек. Проигрывает тот, кто своим ходом забирает правую верхнюю дольку. Докажите, что при правильной игре выигрывает первый игрок.

Задача 2. На доске написаны натуральные числа 1, 2, ..., n, где n > 1. Двое делают ходы по очереди. За свой ход игрок выбирает число из присутствующих на доске и стирает его, и все его делители, оставшиеся на доске. Выигрывает тот, кто сотрет последнее число. Кто выигрывает при правильной игре?

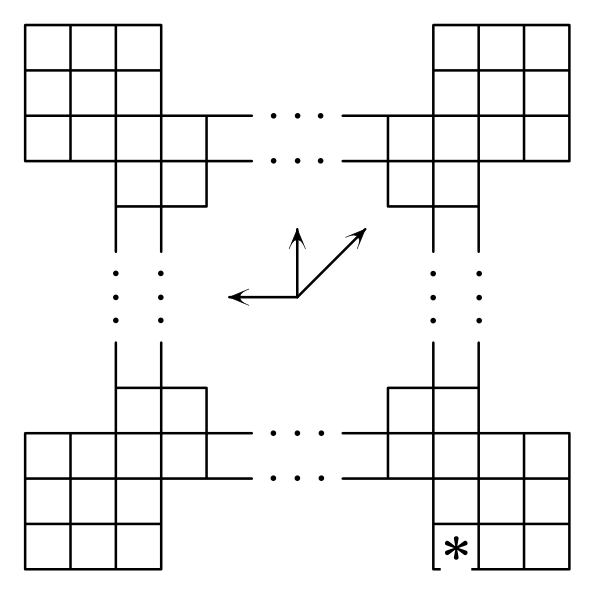
Задача 3. Из квадратной доски 1000×1000 клеток удалены четыре прямоугольника 2×994 (см. рис. 1). На клетке, помеченной звездочкой, стоит кентавр — фигура, которая за один ход может перемещаться на одну клетку вверх, влево или по диагонали вправо и вверх. Двое игроков ходят кентавром по очереди. Проигрывает тот, кто не может сделать очередной ход. Кто выигрывает при правильной игре? (Источник: Всероссийская математическая олимпиада 1992/93, окружной этап, 10 класс)

Задача 4. ("Ним" - нечетное число камней.) Рассмотрим частный случай игры Ним: на доске нечетное число камней. Хорошо известно, что в этом случае у первого игрока есть явная выигрышная стратегия. Предлагается доказать существование этой стратегии в неявном виде.

Задача 4.1. ("Ним") Пусть в игре "Ним" в одной из кучек число камней больше, чем во всех остальных вместе взятых. Аналогично, в этом случае выигрывает первый игрок и можно указать явную стратегию для него. Точно также, предлагается доказать существование этой стратегии в неявном виде.